Notation

Dans le texte, les vecteurs apparaissent écrits en gras. Sur les images, la notation habituelle avec une flèche est respectée.

Définition

Soit un plan orienté par le vecteur unitaire n
Soit un vecteur quelconque u.

Définition des projections orthogonales du vecteur u sur la direction n et sur le plan orthogonal à n.

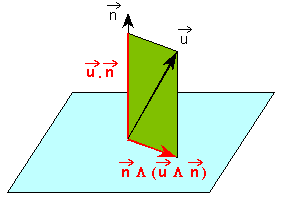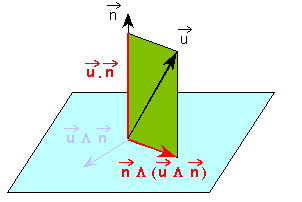
Éléments de démonstration

Le terme u.n correspond à la projection du vecteur u sur la direction n.
La différence u - (n.u).n définit la composante du vecteur u dans le plan orthogonal à n.
Cette différence s'écrit également :

Rappel de la formule du double produit vectoriel :

Appliquée à la dernière expression mise en place, on obtient donc :

Ce qui nous permet de définir le vecteur u comme une somme :

Le premier terme correspond à la composante du vecteur u suivant n,
le deuxième terme correspond à la composante du vecteur u dans le plan orthogonal à n.

Domaine d'application

Cinématique

Définition du pivotement, du roulement, du glissement pour la liaison contact ponctuel.

Une confusion à éviter en cinétique

On retrouve un terme de la forme n Λ (u Λ n) dans la définition de l'opérateur d'inertie, mais son interprétation est différente.