
Plus on est loin,
plus c'est difficile
quand on tourne en rond...
| Introduction : Les acquis de mécanique du point |
| Définition scalaire d'un moment d'inertie |
| Définition vectorielle d'un moment d'inertie |
| Changement d'axe de rotation [Th. de Huygens] |
Convention de notation
Dans le texte, les vecteurs sont notés en gras.
^Introduction
Les acquis de mécanique du point
Soit un point P de masse notée m en mouvement par rapport à un repère R. L'énergie cinétique de ce point dans son mouvement relatif à R s'évalue comme la moitié du produit de sa masse avec le carré de sa vitesse relative. Ce qui s'écrit
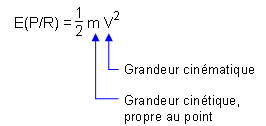
Supposons ce point tournant autour d'un axe fixe (Δ) dans R. On peut écrire à chaque instant V = Rω, R étant le rayon du cercle trajectoire, et l'expression de l'énergie cinétique devient
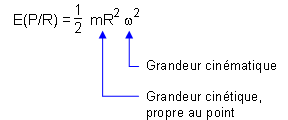
La quantité mR2 est appelée moment d'inertie
de la masse ponctuelle P par rapport à l'axe de rotation (Δ).
^Définition scalaire d'un moment d'inertie
Soit un solide S de masse m
Soient (Δ) un axe de ce solide S, Q un point quelconque de cet axe et δ un vecteur unitaire orientant cet axe.
Soit P un point courant de ce solide, de masse dm situé à la distance courante r de l'axe (Δ).
Notation
Il est conseillé de nommer un moment d'inertie en ajoutant la droite en indice.
Le moment d'inertie du solide S par rapport à l'axe (Δ) est ainsi noté IΔ ou IQδ
Définition
Le moment d'inertie du solide S par rapport à un axe (Δ) est la somme des quantités r 2dm .
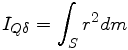
Remarques
Un moment d'inertie caractérise la distribution de la masse autour d'une droite.
Le moment d'inertie IQδ caractérise la répartition de la masse du solide S par rapport à l'axe (Δ).
L'unité d'un moment d'inertie est le kilogramme mètre carré [kg.m2]
^Définition vectorielle d'un moment d'inertie
On reprend les données de la définition précédente sur une figure
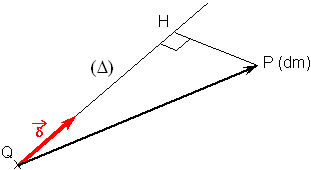
La définition scalaire du moment d'inertie permet d'écrire
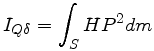
Alors que la distance QH s'évaluerait à l'aide du produit scalaire δ.QP, la distance HP s'évalue à l'aide du produit vectoriel δΛQP
![]()
L'utilisation des propriétés du produit mixte conduit à une autre écriture de cette intégrale
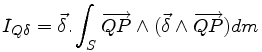
Cette dernière équation laisse apparaître le produit scalaire du vecteur δ avec le vecteur «opérateur d'inertie au point Q du solide S appliqué au vecteur δ»
![]()
Le moment d'inertie du solide S par rapport à un axe (Δ) s'évalue simplement
à partir de l'opérateur d'inertie du solide S calculé en un point Q de l'axe.
Les propriétés et l'écriture matricielle de l'opérateur d'inertie font l'objet d'un chapitre particulier.
^Changement d'axe de rotation [Théorème de Huygens]
Enoncé du théorème
Soit un solide indéformable S de masse m, de centre de masse G.
Soit (Δ) = (Q,δ) une droite de ce solide S et soit d la distance du point G à cet axe.
Le moment d'inertie du solide S par rapport à un axe de rotation (Δ) est égal à la somme
du moment d'inertie de ce solide par rapport à l'axe de rotation parallèle passant par le centre de masse G
et du moment d'inertie du point G affecté de la masse totale m par rapport à (Δ).
![]()
^Moments d'inertie pour des solides courants
Tous les solides considérés ci-dessous sont supposés homogènes, de masse linéïque, surfacique ou volumique ρ.
^Tige de longueur L et de masse m
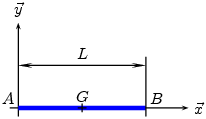 |
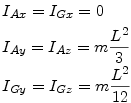 |
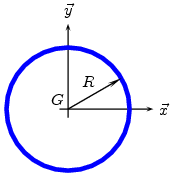
^Cercle de rayon R et de masse m
 |
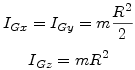 |
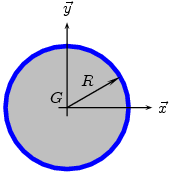
^Disque de rayon R et de masse m
 |
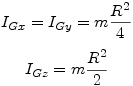 |
^Sphère creuse de rayon R et de masse m
^Sphère pleine de rayon R et de masse m
|
- 303209 -
|