
| Définition |
| Matrice associée à l'opérateur d'inertie |
| Changement de points |
Convention de notation
Dans le texte, les vecteurs sont notés en gras.
E désigne l'espace vectoriel de dimension 3 associé à l'espace géométrique de travail.
^Définition
Soient un solide indéformable S et un point quelconque Q de ce solide.
On appelle opérateur d'inertie au point Q du solide S l'application
qui à tout vecteur δ associe le vecteur ∫S QP Λ(δΛQP) dm
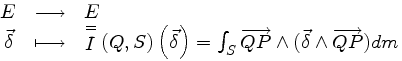
L'opérateur d'inertie définit la répartition de la masse d'un solide indéformable autour d'un de ses points.
^Matrice associée à l'opérateur d'inertie
Soit un solide S auquel on attache une base vectorielle (x, y, z).
Soit Q un point quelconque du solide S, mais fixe une fois choisie.
Soit P un point courant de ce solide, de masse dm et de coordonnées (x, y, z) dans le repère (Q, x, y, z).
La matrice associée à l'opérateur QPΛ... s'écrit
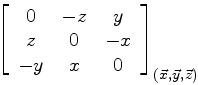
La matrice associée à l'opérateur QPΛ(QPΛ...)s'écrit alors comme le carré de la matrice précédente, ce qui donne après développement
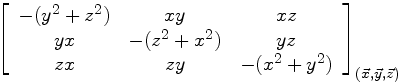
On en déduit l'expression générale de la matrice de l'opérateur d'inertie dans la base (x, y, z)
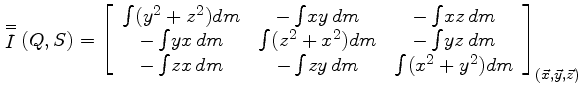
Cette forme intégrale est rarement écrite en l'état. On lui préfère une des deux notations présentées ci-dessous
Notations courantes
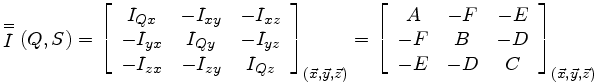
Les termes de la diagonale s'interprètent immédiatement comme des moments d'inertie particuliers
Les termes hors diagonales sont appelés produit d'inertie et sont interprétés lors de l'étude de l'équilibrage dynamique d'un solide en rotation.
Propriété de la matrice d'inertie
La matrice de l'opérateur d'inertie, exprimée dans une base quelconque, est symétrique donc diagonalisable. Il existe ainsi trois valeurs propres et trois vecteurs propres.
Les trois valeurs propres sont appelées moments d'inertie principaux, les droites issues du point de calcul Q et orientées par les vecteurs propres sont appelées axes principaux d'inertie.
^Changement de points
Soit un solide indéformable S de masse m et de centre de masse G.
Supposons connu l'opérateur d'inertie de ce solide S en un point quelconque Q.
L'opérateur d'inertie d'un solide S calculé en un point quelconque Q
est égal à la somme
de l'opérateur d'inertie de ce solide calculé au centre de masse G
et de l'opérateur d'inertie calculé au point Q du solide ponctuel G affecté de la masse totale m du solide S.
![]()
^Matrices d'inertie pour des solides de formes courantes
Tous les solides cités ci-dessous sont supposés être homogène et de masse m.
^Solide présentant un plan de symétrie
Soit un solide indéformable S homogène admettant par exemple le plan (x, Q, y) comme plan de symétrie. Pour chaque point de coordonnées (x, y, z) du solide existe le point de coordonnées (x, y, -z) également sur le solide. Les intégrales ∫Sxz dm et ∫Syz dm sont en conséquences nulles
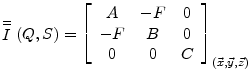
^Solide de révolution
Soit un solide indéformable S homogène admettant par exemple l'axe (Q, z) comme axe de révolution. Tout plan contenant la droite (Q, z) est plan de symétrie pour ce solide. La matrice de l'opérateur d'inertie est donc diagonale dans la base (x, y, z). De plus, pour tout vecteur u orthogonal au vecteur z, le moment d'inertie autour de l'axe (Q, u) est invariant.
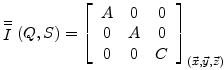
^Tige
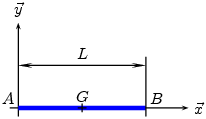 |
|
^Disque
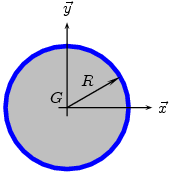 |
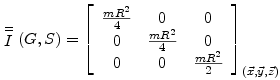 |
|
- 32295 -
|