Composition des vecteurs accélération

[version imprimable (pdf-22Ko)]

Énoncé du problème

Est-il possible d'écrire une relation simple de composition des vecteurs accélérations ?

Étude d'un mouvement

Soit un solide 3 en mouvement par rapport à 2, lui même en mouvement par rapport à 1.
Pour tout point P fixe dans 3 à chaque instant et par définition du vecteur accélération

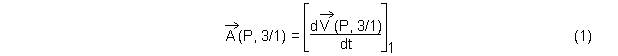
Par composition des vecteurs vitesses

L'opérateur de dérivation vectorielle est un opérateur linéaire. Le vecteur accélération recherché est donc à calculer comme somme de deux termes

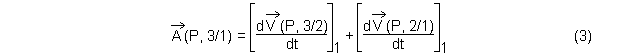
Calcul du premier terme

La formule de dérivation vectorielle permet d'écrire:

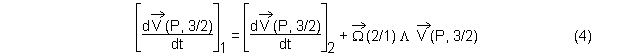
Par définition du vecteur accélération, et comme le point P est fixe dans 3 à chaque instant

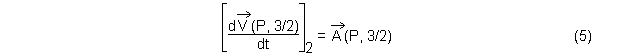
Le premier terme recherché est donc de la forme

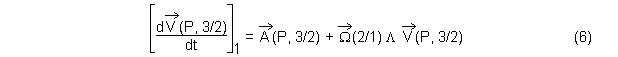
Calcul du second terme

Le calcul de ce terme est plus délicat, car le point P n'est pas fixe dans 2 à chaque instant.
Il s'agit du point de 2 coïncidant à l'instant t considéré avec le point P fixe dans 3, tel que cela a été étudié lors de la composition des vecteurs vitesses.

Pour résoudre ce problème, la méthode la plus simple à mettre en œuvre est d'effectuer le calcul en considérant un point fixe dans 2 à chaque instant, et à comparer le résultat avec celui obtenu lors de l'étude du champ des vecteurs accélérations :

Soit I ce point fixe dans 2 à chaque instant

Il est donc nécessaire de déterminer deux nouveaux termes, car

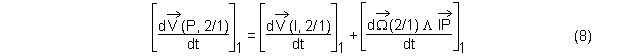
Par définition du vecteur accélération, et comme le point I est fixe dans 2 à chaque instant

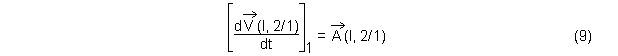
Par ailleurs, en utilisant la formule de dérivation d'un produit

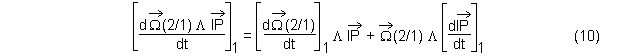
La formule de dérivation vectorielle permet d'écrire immédiatement

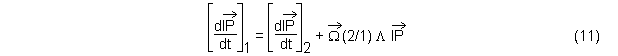
Le point P est fixe à chaque instant dans 3 et le point I est fixe à chaque instant dans 2. On a donc, par définition du vecteur vitesse

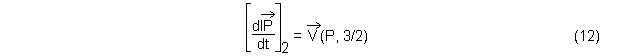
Après les différentes substitutions, l'expression détaillée du terme recherché devient

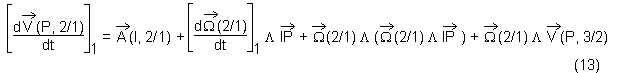
Si le point P était un point fixe à chaque instant dans 2, on aurait la relation vue lors de l'étude du champ des vecteurs accélérations, à savoir

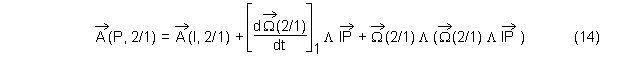
On en déduit la forme finale du second terme recherché

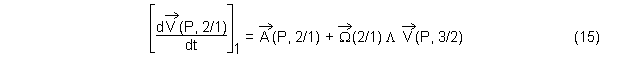
Conclusion

La composition des vecteurs accélérations s'écrit

avec :

	Vecteur accélération du point P dans le mouvement de 3 par rapport à 1.
	Vecteur accélération du point P dans le mouvement de 3 par rapport à 2.
	Vecteur accélération du point P s'il était immobile dans 2 au cours du temps, dans le mouvement de 2 par rapport à 1.
	Accélération complémentaire, appelée accélération de Coriolis, due au mouvement du point P dans un repère lui-même en rotation.