Soit l'espace orienté par la normale sortante de la feuille. Ce choix définit pour le plan de la feuille le sens de rotation positif.

Soit un triangle ABC. Les côtés opposés aux sommets A, B et C sont respectivement de longueur a, b et c. Les angles intérieurs aux sommets A, B et C sont posés positifs est sont respectivement notés α, β et γ.

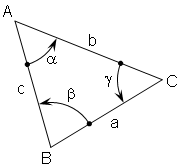
Toutes les relations possibles entre les paramètres géométriques sont issues soit de l'équation scalaire de fermeture angulaire, soit de l'équation vectorielle dite de fermeture géométrique.

Equation scalaire de fermeture angulaire

La somme des angles intérieurs orientés est égale à 180°

α + β + γ = π

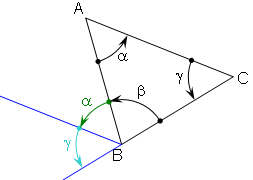
Cette relation se généralise à tout polygone plan.
La somme des angles intérieurs d'un polygone à n côtés est égale à (n-2) x 180°

Equation vectorielle de fermeture géométrique.

Cette équation se généralise à tous les polygones, qu'ils soient plans ou gauches.

Application : Relation de pythagore généralisé

On cherche une relation entre les longueurs des côtés et un seul des angles, par exemple α. Cette relation s'obtient immédiatement à partir de l'équation vectorielle de fermeture géométrique, en la mettant sous la forme

Elevée au carré, cette équation devient

Ce qui donne, après substitution