
Voici une histoire bien champêtre :
en mécanique, le vecteur est au point
ce que la tige qui pousse est à la graine semée...
| Vecteur |
| Champ de vecteurs |
| Champ de vecteurs équiprojectif |
| Torseur |
Convention d'écriture
Dans le texte, les vecteurs apparaissent écrits en gras. Sur les images, la notation habituelle avec une flèche est respectée.
Un vecteur est un élément d'un espace vectoriel.
En mécanique du solide, l'espace géométrique de travail est de dimension 3, et dans un espace vectoriel de dimension 3, tracer des flèches pour imager les vecteurs utilisés est souvent commode.
Dans tout ce site et sauf mention contraire, l'espace vectoriel de travail est un espace de dimension 3.
Un champ de vecteurs est une application qui à tout point de l'espace fait correspondre un vecteur.
On note M(P,t), ou plus souvent M(P) la valeur de ce champ de vecteurs au point P à l'instant t et on attache conventionnellement le représentant de ce vecteur au point P.

En cinématique, ce champ de vecteurs est le champ des vecteurs vitesse. C'est le champ de vecteurs le plus facile à imaginer.
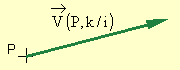
Pour les actions mécaniques, ce champ de vecteurs est le champ des vecteurs moment.
En cinétique,
ce champ de vecteurs est le champ des vecteurs moment cinétique.
En
dynamique, ce champ de vecteurs est le champ des vecteurs moment dynamique.
Champ de vecteurs équiprojectifs
Un champ de vecteurs équiprojectifs est un champ de vecteurs vérifiant la propriété suivante
![]()
Le champ des vecteurs vitesse d'un solide indéformable est un champ de vecteurs équiprojectifs. Cela vient de la définition d'un solide indéformable S :
![]()
Le vecteur AB étant de norme constante au cours du temps, sa seule évolution possible dans un référentiel donné est un changement de direction, ce qui se traduit par le fait que la différence V(A,S/R)-V(B,S/R) soit orthogonale à AB.
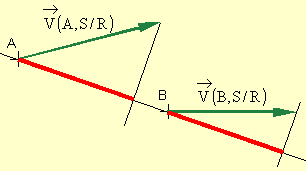
Un torseur est un champ de vecteurs équiprojectifs.
Tout champ de vecteurs équiprojectifs est une application linéaire antisymétrique. Dans un espace de dimension 3, les coefficients de la matrice antisymétrique, dans une des bases qui convient, permettent de définir les coordonnées dans cette même base d'un unique vecteur R. À l'écriture matricielle est substituée une écriture vectorielle faisant intervenir l'opérateur R Λ .
![]()
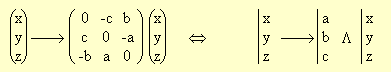
En cinématique du solide
indéformable, l'application linéaire antisymétrique est la
dérivation par rapport au temps dans une base d'observation. L'opérateur
vectoriel est alors "Ω Λ".
Soient deux points A et B d'un solide indéformable i et soit k une base
d'observation de leur évolution, on a:
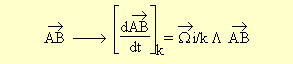
Ce qui permet, en introduisant un point quelconque fixe dans i, d'obtenir la relation fondamentale suivante :
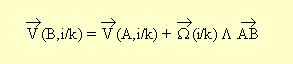
Cette relation se généralise sur tout champ de vecteurs équiprojectifs M(P) :
![]()
Pour retenir cette relation, il suffit de se rappeler que l'on part du vecteur M(A) pour définir le vecteur M(P), donc que l'on va de A vers P.
Un torseur, c'est à dire un champ de vecteurs équiprojectifs, peut donc être construit à partir des deux vecteurs R et M(A). Ces vecteurs sont appelés éléments de réduction du torseur en A.
|
- 57027 -
|