
Quand on dérive loin de sa base,
on se perd inexorablement !
| Formule de dérivation vectorielle |
| Interprétation géométrique |
| Exemple d'utilisation |
Convention d'écriture : Dans le texte, les vecteurs sont tapés en gras
^ Formule de dérivation vectorielle
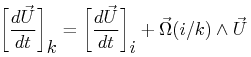
La dérivée par rapport au temps d'un vecteur U(t) dans une base k se calcule à partir de sa dérivée dans une base i et du vecteur rotation du mouvement i/k.
^ Interprétation géométrique
Soit U(t) = λ(t) u(t) un vecteur quelconque, u(t) étant un vecteur unitaire.
Au cours du temps et par rapport à une base d'observation, ce vecteur peut changer soit de module, soit de direction, ce qu'exprime très bien la formule de dérivation d'un produit de fonctions.
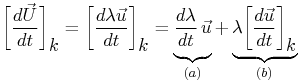
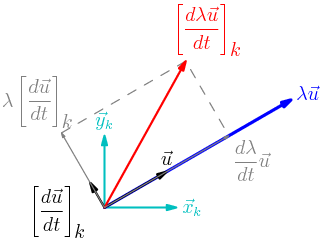
On peut représenter ces différents termes dans la base vectorielle k
^ Exemple d'utilisation
Soit un vecteur AP défini par
![]()
On considère trois bases vectorielles déduites les unes des autres par rotation comme le précisent les deux figures de calcul suivantes
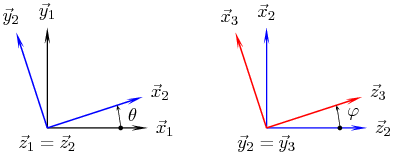
Si l'on s'intéresse à la vitesse de variation du vecteur AP dans la base 1, on écrit
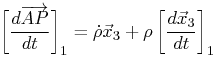
Il est nécessaire de détailler le calcul de la dérivée du vecteur unitaire x3
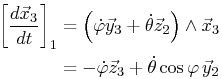
On obtient alors comme résultat final
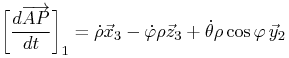
|
- 152341 -
|