
Où l'on peut être inerte
sans pour autant être à la masse :-)
| Définition de la masse |
| Système à masse conservative |
| Centre de masse |
| Méthodes pratiques de détermination du centre de masse |
Convention de notation
Pour cette fiche , un système matériel quelconque est noté Σ, un solide indéformable S.
Le point courant du système est noté P, un point quelconque, mais fixé une fois choisi, est noté Q.
^Définition de la masse
La masse est une grandeur scalaire positive associée à un système matériel.
En mécanique classique, cette masse est représentative de la quantité de matière contenue dans le système matériel.
Propriétés
La masse définit une mesure complètement additive :
Soient Σ1 et Σ2 deux systèmes matériels quelconques mais disjoints de masses respectives m1 et m2.
Le système Σ = Σ1 U Σ2 est de masse m = m1 + m2.
^Système à masse conservative
Un système à masse conservative est un système dont la masse ne varie pas au cours du temps.
Conséquence
Pour un système Σ à masse conservative, la dérivée par rapport au temps de l'intégrale d'une fonction f quelconque du point courant P et du temps t est égale à l'intégrale de la dérivée de cette même fonction par rapport au temps
![]()
^Centre de masse
Soient un système matériel quelconque Σ, de masse m, et P un point courant de ce système, de masse dm.
Le centre de masse d'un système matériel quelconque Σ
est le point noté G défini à partir d'un point quelconque Q par
![]()
Propriété 1
En mécanique classique, le centre de masse est également appelé centre de gravité, ou centre d'inertie du système Σ.
Propriété 2
Soient Σ1 et Σ2 deux systèmes matériels quelconques mais disjoints de masses respectives m1 et m2.
Soient G1 et G2 les centres de masse respectifs des systèmes Σ1 et Σ2.
Soit G le centre de masse du système Σ = Σ1 U Σ2 de masse m = m1 + m2.
Soit Q un point quelconque.
Le point G vérifie
![]()
Propriété 3
Soit G le centre de masse d'un système Σ de masse m.
Soit P un point courant de ce système, de masse dm, en mouvement par rapport à un repère R.
Les vecteurs vitesse et accélération du centre de masse G par rapport au repère R se déduisent des vecteurs vitesses et accélérations des points P par les relations
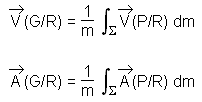
Propriété 4
Soient un solide indéformable S de masse m et G son centre de masse.
Ce point G est un point du solide S.
^Détermination du centre de masse
Par ses coordonnées
Cette méthode est toujours applicable, donc n'est à utiliser qu'en tout dernier ressort.
Par symétrie
Soit un solide indéformable S et homogène admettant
le centre de masse est respectivement situé
Comme barycentre...
... de centres de masse connus de volumes élémentaires, pondérés de leurs masses respectives.
Exemple
Soit un solide (D), homogène, d’épaisseur négligeable, de masse surfacique ρ et de masse totale m. Ce solide est formé d’un disque plein (D1) percé d’un disque (D2).
Déterminer la position du centre d’inertie G de ce solide.
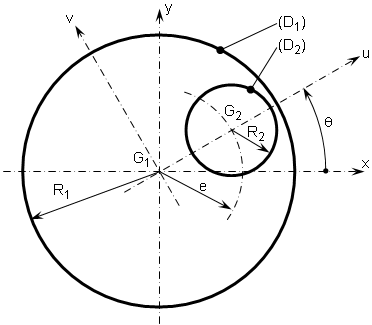
Le centre de masse G du solide (D) est le barycentre des centres de masse des disques (D1) et (D2) affectés respectivement des coefficients +m1 et -m2, ce qui donne, tout calcul fait
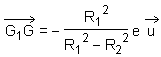
|
- 91374 -
|