
| Définition |
| Conséquences |
Soit un solide S de centre de masse G en rotation autour d'un axe (Δ) fixe dans un référentiel assimilable à un référentiel galiléen.
^Définition
Soit un solide S de centre de masse G en rotation autour d'un axe (Δ) fixe dans un référentiel assimilable à un référentiel galiléen.
Un solide est dit équilibré lors de sa rotation autour d'un axe fixe si et seulement si
son centre de masse est sur l'axe de rotation
et l'axe de rotation est un axe principal d'inertie pour ce solide.
Equilibrage statique et équilibrage dynamique
Ces deux termes apparaissent dans la littérature :
La distinction ainsi faite ne présente que peu d'intérêt. Parler d'«équilibrage d'un solide en rotation» implique son équilibrage dynamique.
^Conséquences
Les deux conditions d'équilibrage énoncées entraînent des contraintes pour deux des trois coordonnées du centre de masse du solide considéré, et pour deux des trois produits d'inertie de la matrice de l'opérateur d'inertie du même solide.
Supposons le centre de gravité G sur l'axe de rotation (Δ) : Il peut être n'importe où sur cet axe.
On peut maintenant en déduire la forme de la matrice de l'opérateur d'inertie au point G, de manière à ce que l'axe (Δ) soit axe principal d'inertie.
![]()
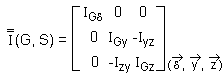
|
- 15400 -
|