
| Définition géométrique |
| Définition cinématique |
| Identifier un mouvement de translation |
^ Définition géométrique
Soit un mouvement i/k.
On rappelle ici l'équivalence solide-repère-espace : Ces trois mots sont employés indifféremment.
Le solide i est dit en translation par rapport au solide k
si et seulement si
toute droite du solide i conserve par rapport à k une direction constante au cours du temps.
Remarque
Soit à un instant t une droite du solide k parallèle à la droite choisie sur i.
Ces deux droites restent parallèles au cours du temps
Conséquence
Cette définition induit des trajectoires semblables pour tous les points de i dans leur mouvement par rapport à k. Elles se déduisent les unes des autres par simple translation.
^ Définition cinématique
En mécanique du solide, un mouvement de translation est un mouvement
pour lequel le vecteur rotation est le vecteur nul.
Soit un solide i en mouvement de translation par rapport à un solide k, le torseur cinématique associé au mouvement i/k est un torseur couple
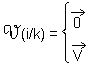
Conséquence
Pour un mouvement de translation, le champ des vecteurs vitesses est un champ uniforme de vecteur. À chaque instant, tous les vecteurs vitesses sont identiques.
Remarque
La conséquence énoncée ne veut évidemment pas dire que les vecteurs vitesses ne changent pas au cours du temps !
^ Identifier un mouvement de translation
Pour montrer que le mouvement d'un solide i par rapport à un solide k est un mouvement de translation, il suffit de montrer que le vecteur rotation pour le mouvement considéré est le vecteur nul.
![]()
Pour éventuellement caractériser ce mouvement de translation, il suffit d'identifier la nature de la trajectoire d'un point quelconque dans le mouvement considéré.
|
- 25157 -
|