
Liste des mots-clés à comprendre, apprendre et savoir utiliser
| Point coïncidant |
| Trajectoire |
| Vecteur-position |
| Vecteur-vitesse |
| Vecteur-accélération |
Soit un point P(t) mobile
dans un espace affine E muni d'un repère R.
L'espace E est l'ensemble
des points Mi fixes (ou immobiles) par rapport à R.
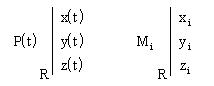
^ Point coïncidant
A l'instant
t, il existe un point Mt fixe dans R confondu avec le point P(t).
Le point Mt est appelé point coïncidant avec P(t) dans
le repère R à l'instant t.
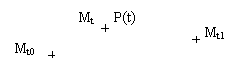
^ Trajectoire
La trajectoire du point P(t) dans son mouvement par rapport au repère R est l'ensemble des points coïncidants dans E.
Une trajectoire est définie relative à un repère
^ Vecteur-position
La position du point P(t) dans l'espace E est modélisée par un vecteur construit à partir d'un point fixe dans R.
![]()
Ce vecteur est nommé vecteur-position du point P(t) dans le repère R.
^ Vecteur-vitesse
On appelle vitesse
du point P(t) dans son mouvement par rapport à R le taux de variation de
la position du point P(t) dans R.
Elle est modélisée par un
vecteur défini par la dérivée du vecteur-position du point
P(t) dans R :
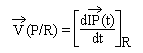
Ce vecteur est nommé vecteur-vitesse du point P(t) dans le repère R.
Le vecteur-vitesse est tangent à la trajectoire de P dans R.
Une interprétation possible du vecteur-vitesse :
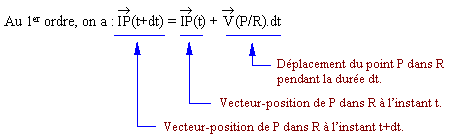
^ Vecteur-accélération
On appelle accélération du point P(t) dans son mouvement par rapport
à R le taux de variation de la vitesse du point P(t) dans R.
Elle est modélisée
par un vecteur défini par la dérivée du vecteur-vitesse du point P(t) dans R :
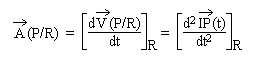
Ce vecteur est nommé vecteur-accélération du point P(t) dans le repère R.
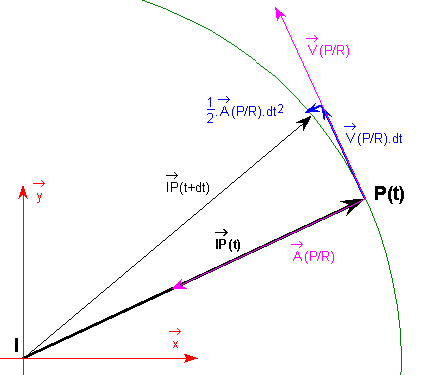
Une interprétation possible du vecteur-accélération

Application à un point P en mouvement de rotation uniforme autour de l'axe (I, z)
|
- 18236 -
|