
«Appuyez-vous sur les principes,
ils finiront bien par céder !»
Oscar Wilde
«Principe fondamental de la statique»
| Théorèmes de l'équilibre |
| Définitions annexes |
| Réciproque des théorèmes de l'équilibre |
| Méthodologie de résolution d'un problème de statique |
| Exemple : bras de robot |
^Théorèmes de l'équilibre
Solide indéformable
Soit un solide indéformable S dont on constate ou on souhaite l'équilibre par rapport à un référentiel galiléen Rg.
SI un solide indéformable S est en équilibre dans un référentiel galiléen,
ALORS le torseur des actions mécaniques extérieures au solide S
est à chaque instant le torseur nul.
![]()
Système matériel quelconque
Ce théorème se généralise à un système matériel quelconque Σ, dont on constate ou on souhaite l'équilibre par rapport à un référentiel galiléen Rg.
SI un système matériel Σ est en équilibre dans un référentiel galiléen,
ALORS le torseur des actions mécaniques extérieures au système Σ
est à chaque instant le torseur nul.
![]()
^Définitions annexes
Équilibre
Un équilibre est un mouvement nul.
Dans le cas d'un solide indéformable, un mouvement nul est un mouvement dont le torseur cinématique correspondant est à chaque instant le torseur nul.
Dans le cas d'un système matériel quelconque, un mouvement nul se traduit par un champ des vecteurs vitesses nul.
Référentiel galiléen
Un repère galiléen est le repère de référence en mécanique newtonienne. Il est supposé exister lors de l'énoncé du principe fondamental de la dynamique, mais on n'en connaît que des approximations plus ou moins fines. Ce sont les repères héliocentrique, géocentrique, terrestre...
Par ailleurs, le temps est supposé être le même en tout lieu de l'espace.
Milieu environnant
Le milieu environnant d'un système quelconque est composé de tous les éléments de l'univers autres que le système, supposés être en relation avec ce dernier.
^Réciproque des théorèmes de l'équilibre
La réciproque des théorèmes de l'équilibre est fausse
Une seule proposition peut être formulée, concernant tous les systèmes matériels, solides ou quelconques.
Système matériel
Si à chaque instant, le torseur d'actions mécaniques extérieures de toute partie d'un système matériel Σ est le torseur nul, alors il existe un référentiel galiléen dans lequel ce système matériel Σ est en équilibre.
![]()
Cette proposition est dans les faits peu exploitable, car la nullité du torseur des actions mécaniques extérieures doit être vérifiée quelle que soit la partie incluse...
^Méthodologie de résolution d'un problème de statique
1. Choix du système dont on étudie l'équilibre.
Le graphe des liaisons permet de dénombrer quelques choix possibles.
La théorie des mécanismes permet de dénombrer les équations scalaires nécessaires.
2. Inventaire du milieu environnant au système.
Cet inventaire doit être exhaustif.
Il est donc fortement conseillé de commencer par la simple recherche des objets ou des phénomènes ayant une influence sur le comportement du système.
Le choix des modèles d'actions mécaniques retenus se fait avec profit dans un deuxième temps.
Cet inventaire se termine par un bilan des nombres d'équations et d'inconnues scalaires du problème, ce qui permet d'émettre un avis sur les possibilités de résolution.
3. Choix d'une stratégie de calcul
L'écriture systématique de toutes les équations scalaires n'est en général pas utile et est de plus rédhibitoire. Elle est donc à proscrire.
La recherche de l'équation scalaire pertinente pour trouver simplement une composante est à mettre en oeuvre systématiquement. Elle demande un peu de réflexion préliminaire, mais permet d'économiser des lignes et des lignes de calculs trop souvent inutiles.
^Exemple
Soit un mécanisme dont on élabore le graphe des liaisons.
Par exemple ici un bras de robot pour lequel les axes sont motorisés et une charge accrochée à l'extrémité C du bras 3. On s'intéresse aux valeurs des couples moteurs nécessaires au maintien de l'équilibre de la charge.
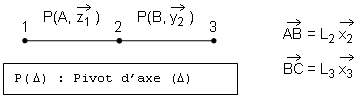
On suppose le repère attaché à 1 assimilable à un repère galiléen.
Les actions de l'air et de la pesanteur sur les pièces du mécanisme sont négligées devant l'action de la charge.
La théorie des mécanismes permet de dire qu'une étude systématique nécessite l'écriture de 12 équations scalaires.
Par ailleurs, trois équilibres sont ici possibles à l'étude :
Deux stratégies sont possibles :
Équilibre étudié |
Nombre . d'inconnues de liaison |
Nombre d'inconnues autres |
Commentaire |
2/1 |
10 |
3 |
Aucune équation n'évite les 10 inconnues de liaison. |
3/1 |
5 |
2 |
L'équation de moment en B scalaire y2 évite les 5 inconnues de la liaison pivot et permet de calculer le couple moteur entre 2 et 3 |
{2, 3}/1 |
5 |
2 |
L'équation de moment en A scalaire z1 évite les 5 inconnues de la liaison pivot et permet de calculer le couple moteur entre 1 et 2 |
|
- 15981 -
|