
| Variable logique |
| Fonction logique |
| Les fonctions logiques d'une seule variable |
| Les fonctions logiques de deux variables |
| Théorèmes |
^Variable logique
Une variable logique est une variable qui ne peut avoir que deux états
En logique des propositions, ces états sont les états VRAI et FAUX. Ces états sont communément appelés valeurs de la variable.
Il existe d'autres associations de deux états possibles, car une variable logique est un modèle adapté à l'étude des phénomènes tout ou rien :
Oui |
Non |
Fermé |
Ouvert |
-5V |
+5V |
etc... |
Il est fort usuel de coder les deux valeurs possibles d'une variable logique avec les chiffres 0 et 1. Néanmoins, il est nécessaire de garder à l'esprit que ces deux valeurs ne sont pas des nombres.
Exemples
Soit un interrupteur à deux positions et soit a la variable logique définissant son état : on associe à chacune des positions un état de la variable.
Interrupteur au repos |
Interrupteur manoeuvré |
|---|---|
0 |
1 |
Soit une ampoule électrique et soit x la variable logique définissant son état :
Lampe éteinte |
Lampe allumée |
|---|---|
0 |
1 |
ATTENTION : Ces deux exemples que l'on vient de décrire ne présument pas de l'état des signaux qui permettent de les obtenir. Une lampe peut être allumée alors que l'interrupteur correspondant est au repos.
Exemple d'erreur à éviter
Soit une porte et soit p la variable logique définissant son état : on aimerait associer à chacune des positions de la porte une valeur de la variable.
Porte Fermée |
|
|---|---|
0 |
1 |
Contrairement à un interrupteur par exemple, une porte non fermée n'est pas une porte ouverte... Il faut une deuxième variable pour définir l'état ouvert !
Ce qui entraîne 2^2=4 états différents possibles pour une porte :
La dernière combinaison surprend, mais c'est ainsi. La combinaison reste possible, même si l'obtenir ne l'est pas.
^Fonction logique
Une fonction logique est une fonction combinatoire définie sur l'ensemble des variables logiques.

La fonction est définie par
une table de vérité,
une équation logique, un tableau
de Karnaugh, ou par un schéma logique.
Toutes ces définitions sont équivalentes.
Nombre de fonctions logiques
Une variable logique x ne peut avoir que deux valeurs, codées par exemple 0 et 1.
Définir une fonction logique d'une seule variable fi(x) revient à définir les deux images fi(0) et fi(1), images elles-mêmes à choisir parmi les valeurs 0 ou 1. On a donc 2^2 combinaisons, soit 4 fonctions possibles.
Définir une fonction logique de deux variables g(x,y) revient à définir les images des quatre combinaisons d'entrées (0,0), (0,1), (1,1) et (1,0) parmi les deux valeurs possibles 0 et 1. On a donc 2^22 combinaisons, soit 16 fonctions possibles.
Le dénombrement se généralise : il existe 2^2n fonctions logiques de n variables.
Autres fonctions
En séquentiel, il existe des fonctions d'une seule variable logique
qui dépendent également du temps.
Attention, dans ce cas, on n'est plus dans le cadre de la seule logique combinatoire.
^Les fonctions logiques d'une seule variable
Il existe quatre fonctions logiques d'une seule variable, à savoir les fonctions OUI & NON, toujours VRAI et toujours FAUX.
a |
0 |
1 |
|
| Toujours faux | f0(a) = 0 |
0 |
0 |
| OUI | f1(a) = a |
0 |
1 |
| NON | f2(a) = /a |
1 |
0 |
| Toujours vrai | f3(a) = 1 |
1 |
1 |
^Les fonctions logiques de deux variables
Il existe seize fonctions logiques de deux variables
| Deux fonctions constantes |
|
| Les fonctions d'une variable |
|
| Les fonctions ET & nonET |
|
| Les fonctions OU & nonOU |
|
| Les fonctions Ou exclusif & Identité |
|
| Les fonctions Inhibition |
|
| Les fonctions Implication |
|
Présentation de quelques unes de ces fonctions sous forme de table de vérité
AND |
NAND |
OR |
NOR |
XOR |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ET |
NonET |
OU |
NonOU |
OUX |
Identité |
Inhibition |
Implication |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
a.b |
/(a.b) |
a+b |
/(a+b) |
a++b |
/(a++b) |
a./b |
/(a./b) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
^Théorèmes
Théorème 1
Toute fonction logique s'exprime en fonction des quatre opérateurs OUI, NON, ET & OU
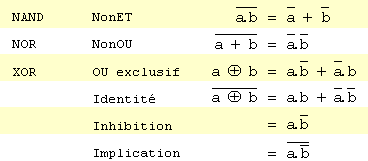
Les deux premières lignes sont connues sous le nom de théorèmes de De Morgan.
Théorème 2
Toute fonction logique s'exprime en fonction des quatre opérateurs OUI, NON, NonET & NonOU.
Théorème 3
Il existe des opérateurs logiques dits "universels" permettant de définir toute fonction logique, par exemple les opérateurs logiques NonET et NonOU.
|
- 30083 -
|